Rimpei Chiba
Theoretical Astrophysicist
Galactic echoes
We considered the possibility that the vertical phase-space spirals discovered by Gaia contain manifestations of "phase-space echoes". First established in plasma physics in the 1960s, echoes arise when a collisionless system is perturbed twice: the macroscopic responses to both perturbations mix to small scales in phase space, whereupon they couple non-linearly, producing a third macroscopic response without the need for a third perturbation. We derive the galactic analogue of the plasma echo theory using angle-action variables and apply it to the vertical motion of stars in the Galactic disk. We find that echoes can survive longer than the original response at late times, since the latter are more tightly wound and hence more vulnerable to destruction by diffusion through orbital scattering off molecular clouds. This implies that some of the observed phase spirals may in fact be echoes, in which case their degree of winding may not indicate the time elapsed since the perturbation.
We considered the possibility that the vertical phase-space spirals discovered by Gaia contain manifestations of "phase-space echoes". First established in plasma physics in the 1960s, echoes arise when a collisionless system is perturbed twice: the macroscopic responses to both perturbations mix to small scales in phase space, whereupon they couple non-linearly, producing a third macroscopic response without the need for a third perturbation. We derive the galactic analogue of the plasma echo theory using angle-action variables and apply it to the vertical motion of stars in the Galactic disk. We find that echoes can survive longer than the original response at late times, since the latter are more tightly wound and hence more vulnerable to destruction by diffusion through orbital scattering off molecular clouds. This implies that some of the observed phase spirals may in fact be echoes, in which case their degree of winding may not indicate the time elapsed since the perturbation.

Gaia recently revealed a two-armed spiral pattern in the vertical phase-space distribution of the inner Galactic disc, indicating that some non-adiabatic perturbation symmetric about the mid-plane is driving the inner disc out of equilibrium. We for the first time show that such two-armed phase spirals can naturally form in the inner disc if there is a vertical resonance that breaks the adiabaticity; otherwise, their formation requires a perturber with an unrealistically short lifetime. In particular, we predict analytically and confirm with particle simulations that a steadily rotating (non-winding) two-armed phase spiral forms near the resonance when stars are subject to both periodic perturbations (e.g. by spiral arms) and stochastic perturbations (e.g. by giant molecular clouds). Due to the presence of multiple resonances, the vertical phase-space exhibits several local phase spirals that rotate steadily at distinct frequencies, together forming a global phase spiral that evolves over time.
Galaxy Zoo CEERS: Bar Fractions Up to z ~ 4.0
We study the evolution of the bar fraction in disk galaxies between 0.5 < z < 4.0 using multiband colored images from JWST Cosmic Evolution Early Release Science Survey (CEERS). We find that the fraction of weak bars decreases with increasing redshift, whereas the fraction of strong bars remains constant between 0.5 < z < 2.5. This implies that disk instabilities, in which bars grow secularly, are the dominant mode of bar formation at lower redshifts, while bar formation through interactions and mergers, in which large strong bars form rapidly, is more common at higher redshifts.
We study the evolution of the bar fraction in disk galaxies between 0.5 < z < 4.0 using multiband colored images from JWST Cosmic Evolution Early Release Science Survey (CEERS). We find that the fraction of weak bars decreases with increasing redshift, whereas the fraction of strong bars remains constant between 0.5 < z < 2.5. This implies that disk instabilities, in which bars grow secularly, are the dominant mode of bar formation at lower redshifts, while bar formation through interactions and mergers, in which large strong bars form rapidly, is more common at higher redshifts.

Exploring the impact of a decelerating bar on transforming bulge orbits into disc-like orbits
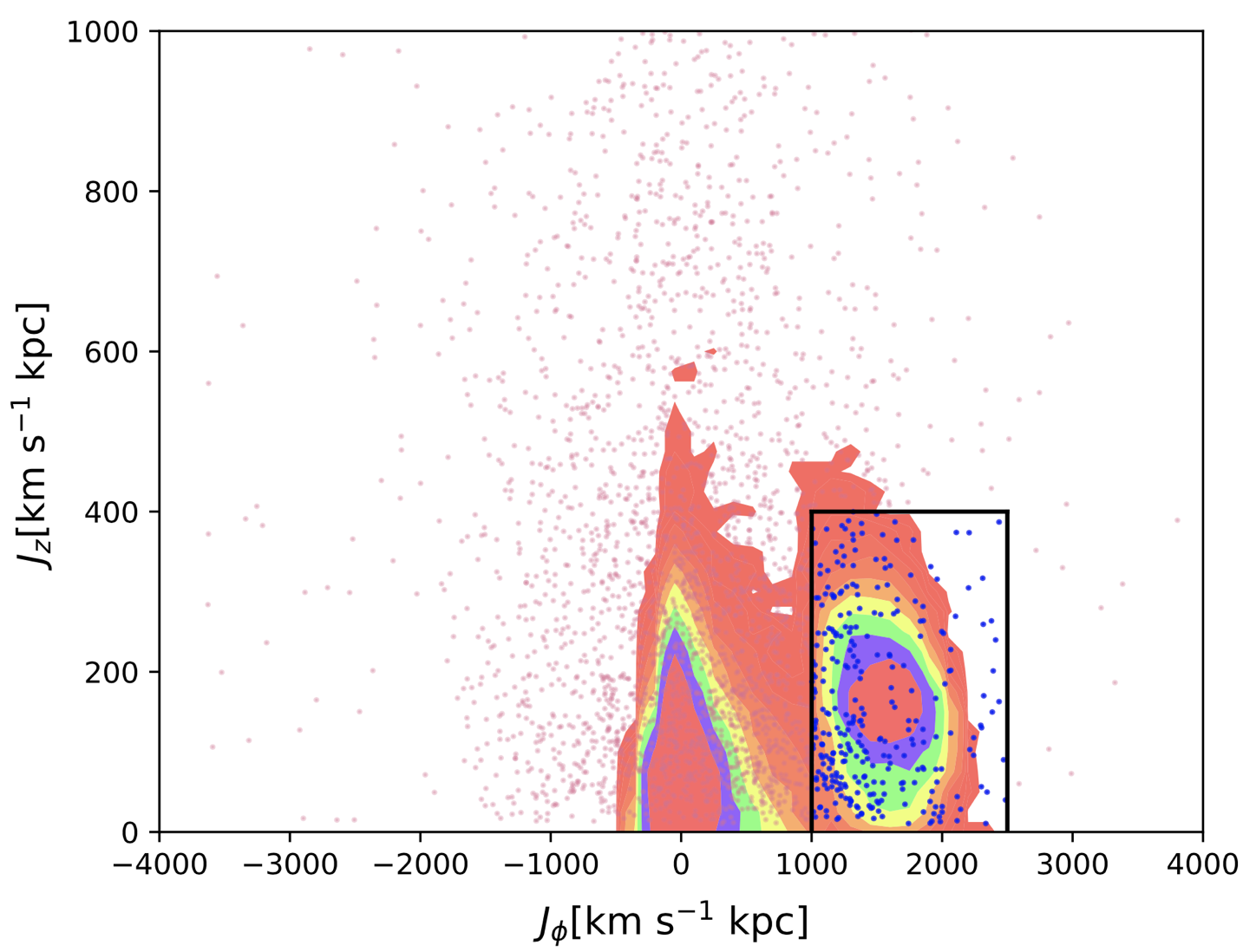
The most metal-poor tail of the Milky Way contains a population of stars with very prograde planar orbits, which is puzzling in both their origin and evolution. We investigated the possibility that the metal poor stars were resonantly dragged by the bar from the inner Galaxy, where many of the old and low-metallicity stars in the Galaxy are located.
The most metal-poor tail of the Milky Way contains a population of stars with very prograde planar orbits, which is puzzling in both their origin and evolution. We investigated the possibility that the metal poor stars were resonantly dragged by the bar from the inner Galaxy, where many of the old and low-metallicity stars in the Galaxy are located.
Origin of reduced dynamical friction by dark matter haloes with net prograde rotation
Dynamical friction has long been known to be suppressed when dark haloes have net rotation in the same direction as the disk. We provided a theoretical explanation to this using both linear and nonlinear theory. The key role is played by the direct-radial resonances, which are strongest when orbits are perpendicular to the galactic plane \((L_z = 0)\). Since spinning halos posses a positive gradient in the distribution function near \(L_{z} = 0\), these resonances exert a strong positive torque on the bar, weakening the overall dynamical friction.
Dynamical friction has long been known to be suppressed when dark haloes have net rotation in the same direction as the disk. We provided a theoretical explanation to this using both linear and nonlinear theory. The key role is played by the direct-radial resonances, which are strongest when orbits are perpendicular to the galactic plane \((L_z = 0)\). Since spinning halos posses a positive gradient in the distribution function near \(L_{z} = 0\), these resonances exert a strong positive torque on the bar, weakening the overall dynamical friction.
Dynamical friction and feedback on galactic bars in the general fast-slow regime
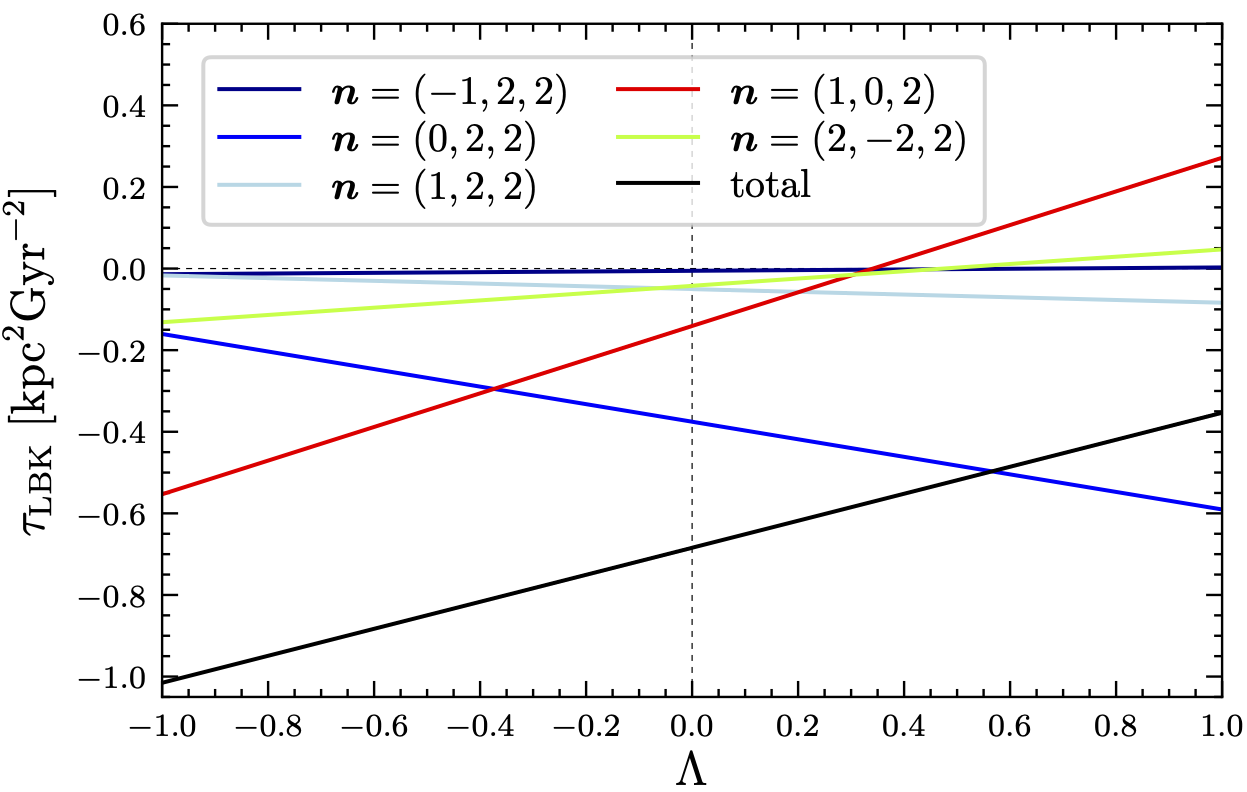
We provided a general theory of dynamical friction on galactic bars in the nonlinear (non-perturbative) regime. Our theory seamlessly connects past theories based on the linear approximation, which is only valid in the fast limit, and the extreme adiabatic approximation, which is only valid in the slow limit (i.e. constant pattern speed). In particular, we derived the complete analytical formula for dynamical feedback, a nonlinear process that transfers energy between waves and particles due to the shift in resonances.
We provided a general theory of dynamical friction on galactic bars in the nonlinear (non-perturbative) regime. Our theory seamlessly connects past theories based on the linear approximation, which is only valid in the fast limit, and the extreme adiabatic approximation, which is only valid in the slow limit (i.e. constant pattern speed). In particular, we derived the complete analytical formula for dynamical feedback, a nonlinear process that transfers energy between waves and particles due to the shift in resonances.
Oscillating dynamical friction on galactic bars by trapped dark matter
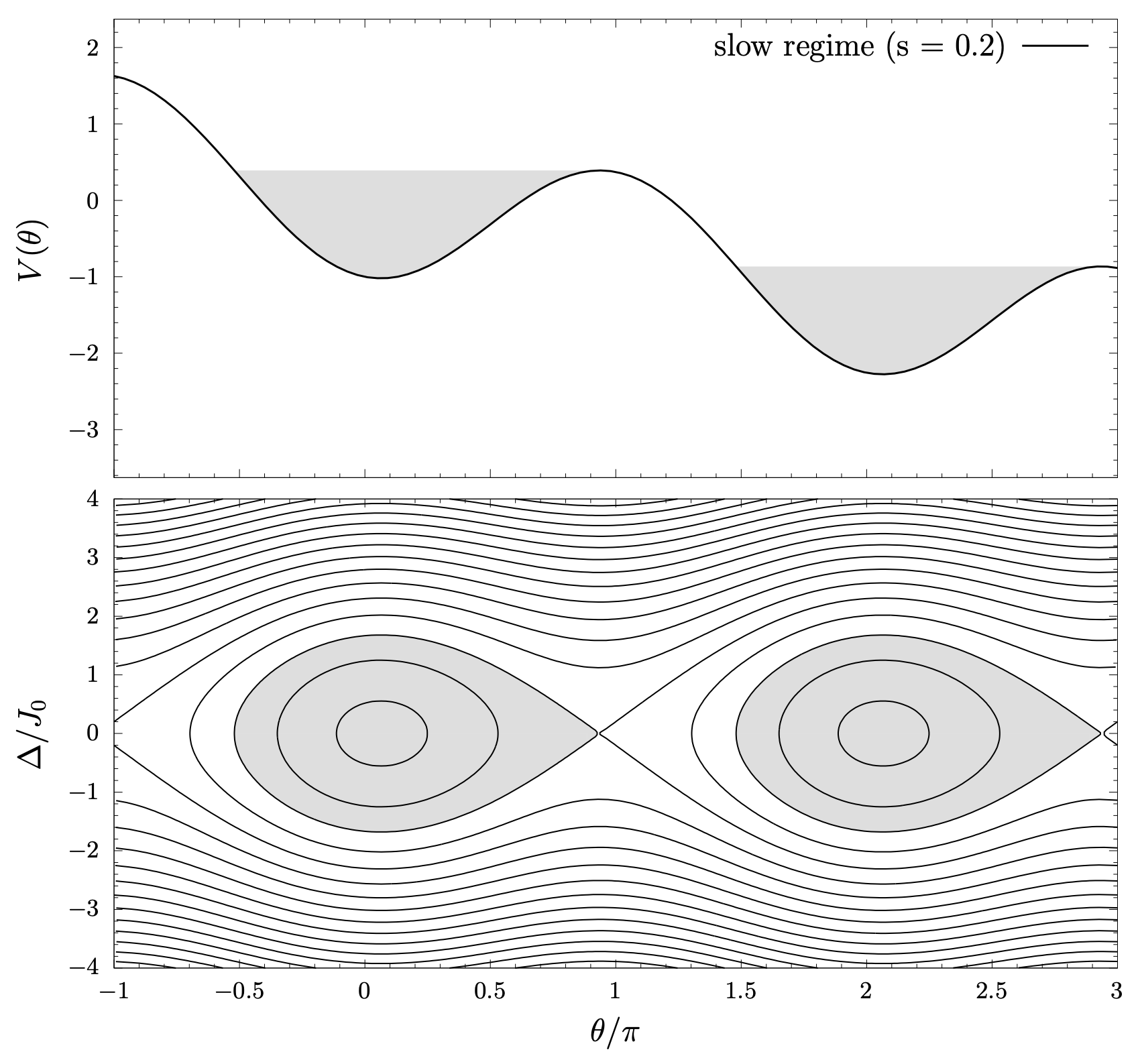
We described the mechanism of dynamical friction in the presence of nonlinear resonant trapping. We showed that, due to the initial gradient in the dark halo's distribution function, net angular momentum is transferred to the halo as trapped particles librate and phase mix. Conventional linear perturbation theory fails to capture this nonlinear behaviour (top). We successfully modeled this process using the resonant angle-action coordinates (bottom) and predicted that dynamical friction on galactic bars may undergo damped oscillation.
We described the mechanism of dynamical friction in the presence of nonlinear resonant trapping. We showed that, due to the initial gradient in the dark halo's distribution function, net angular momentum is transferred to the halo as trapped particles librate and phase mix. Conventional linear perturbation theory fails to capture this nonlinear behaviour (top). We successfully modeled this process using the resonant angle-action coordinates (bottom) and predicted that dynamical friction on galactic bars may undergo damped oscillation.
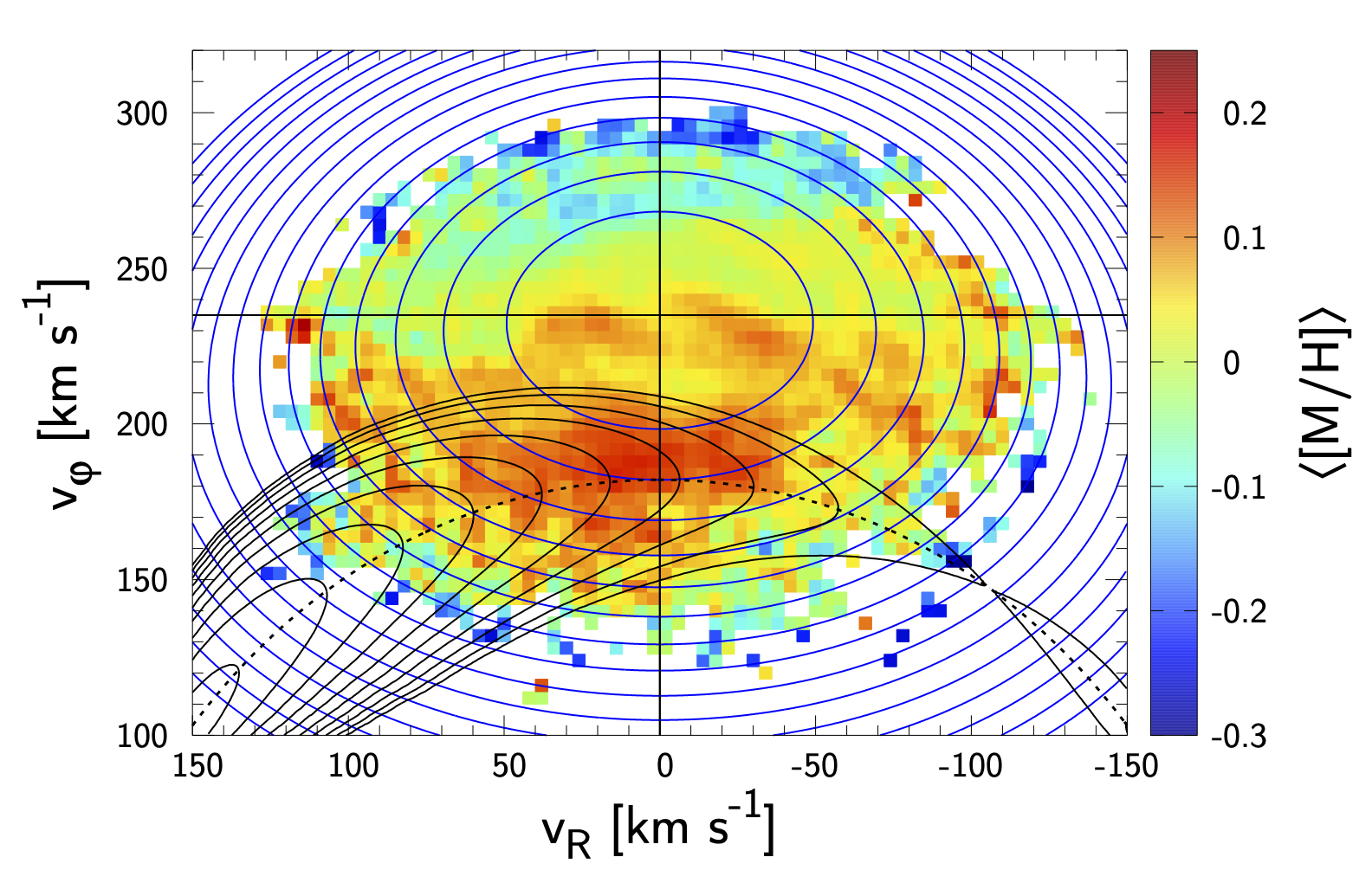
Tree-ring structure of Galactic bar resonance
We identified a "tree-ring structure" in the phase space of the bar's resonance: the resonance grows inside-out with stars captured earlier occupying the core of the resonance. We showed that the local stellar metallicity increases monotonically towards the core of the bar's corotation resonance, indicating that the resonance has migrated from the inner galaxy where the metallicity is higher. This observation corroborates the bar's spin-down and hence the existence of dark matter that must have deprived angular momentum from the bar through dynamical friction.
We identified a "tree-ring structure" in the phase space of the bar's resonance: the resonance grows inside-out with stars captured earlier occupying the core of the resonance. We showed that the local stellar metallicity increases monotonically towards the core of the bar's corotation resonance, indicating that the resonance has migrated from the inner galaxy where the metallicity is higher. This observation corroborates the bar's spin-down and hence the existence of dark matter that must have deprived angular momentum from the bar through dynamical friction.
Resonance sweeping by a decelerating Galactic bar
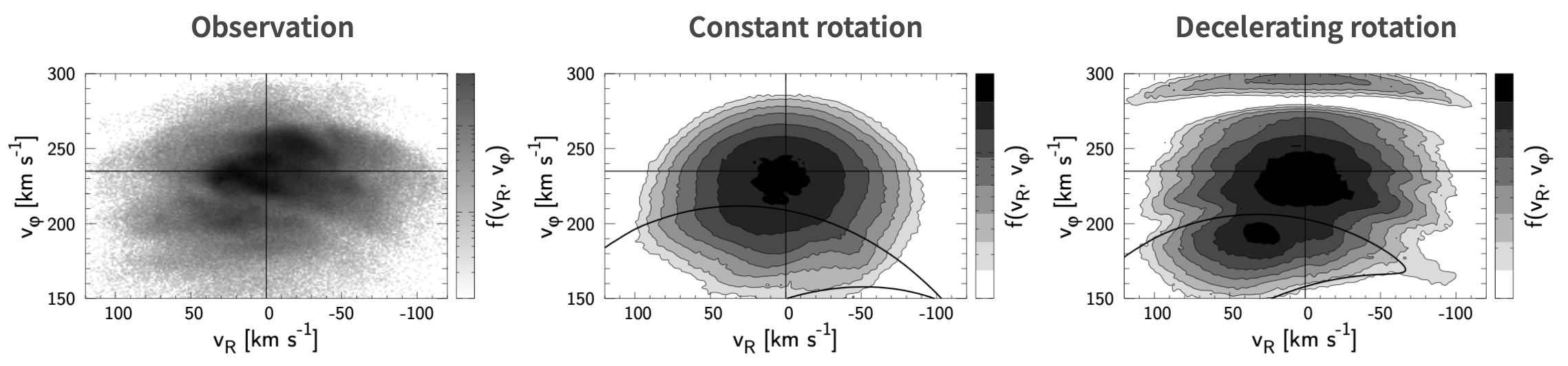
We provided the first observational implication for the spin-down of the Galactic bar from the velocity distribution of Solar neighborhood stars. In particular, we showed that perturbations by a bar spinning down at a rate consistent with ΛCDM models can naturally explain many of the features in the observational data, including the Hercules stellar stream.
We provided the first observational implication for the spin-down of the Galactic bar from the velocity distribution of Solar neighborhood stars. In particular, we showed that perturbations by a bar spinning down at a rate consistent with ΛCDM models can naturally explain many of the features in the observational data, including the Hercules stellar stream.