I am currently in Planck Satellite HFI Core team, EUCLID Satellite theory group, and CMB experiments ACT and SPIDER.

The topics I have been working on are: Second-order Boltzmann code, CMB bispectrum, primordial gravitational waves from inflation (and preheating), primordial non-Gaussianity from preheating (modulated preheating), dark energy parametrization, and cosmological parameter estimation using a variety of observational data (CMB, weak lensing, Type Ia supernovae, galaxy power spectrum, Lya forests).

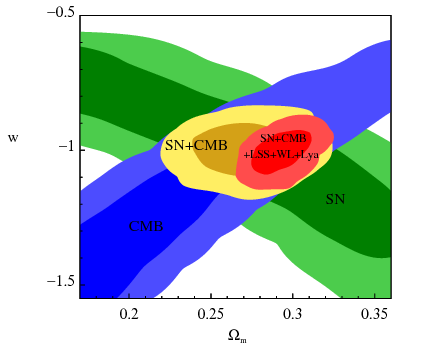
In the past I have modified cosmomc to constrain a variety of interesting models: quintessence/phantom dark energy models, decaying dark matter, Infra-red cascading during inflation. I have also written a weak lensing likelihood code to include the weak lensing data into Mukov Chain Monte Carlo (MCMC) simulation. In the left panel I am showing the equation of state (EOS) of dark energy and the fractional cold dark matter density are constrained by different cosmological data sets. For each data set, the degeneracy between the two parameters causes "cosmic confusion". However, with many complementary cosmological observations, such degeneracy can be broken. The parameters constrained by a combination of the many cosmological observations converge to a concordance model.

Shown in the right panel is the constraint on fractional matter density $\Omega_m$, and $\sigma_8$, a key cosmological parameter describing the amplitude of linear matter power spectrum at scale $8h^{-1}$ Mpc. Althoug little tension between different data sets can be seen in this case, at two sigma (95.4% confidence) level they are consistent with the standard flat $\Lambda$CDM model.

In both plots I have used the latest available data sets in Nov 2009, which include Cosmic Microwave Background data (WMAP 5, Boomerang, Acbar, CBI, MAXIMA, DASI, VSAF, QUAD, BICEP), Weak Lensing data (COSMOS, CFHTLS-wide, RCS, VIRMOS, GaBoDS), Large Scale Structure data (SDSS LRG DR7), and Lyman alpha forest data.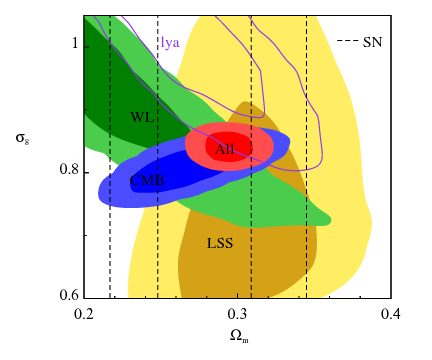

Another thing I have been doing for a while is using lattice simulation to study early universe preheating. I have implemented 4-th, 6-th, and 8-th order symplectic integrator in the lattice simulation code. It now can conserve energy at 10^-12 level for canonical scalar fields simulations. The extension to non-canonical scalar fields is done in August 2009. The key component of the code is a sympletic - Runge-Kutta hybrid integrator, which can conserve energy at 10^-8 level for non-canonical scalar fields simulations (the benchmark models I have tried are Roulette inflation models and Racetrack inflation models). The right panel shows the evolution of Roulette field $\tau_2$ (the real part of last-stablized modulus) on a 2D slice in the lattice simulation box (see our paper arXiv: 0909.0503). The simulation boxsize is 0.006H^-1, where H is the Hubble parameter at the end of inflation.