Research
My research centers on Black Holes, objects with so strong gravity
that nothing can escape, not even light. Black holes and their
properties are predicted by Einstein's theory of General
Relativity, and my main activity are computer calculations of
Einstein's equations to learn about black holes.
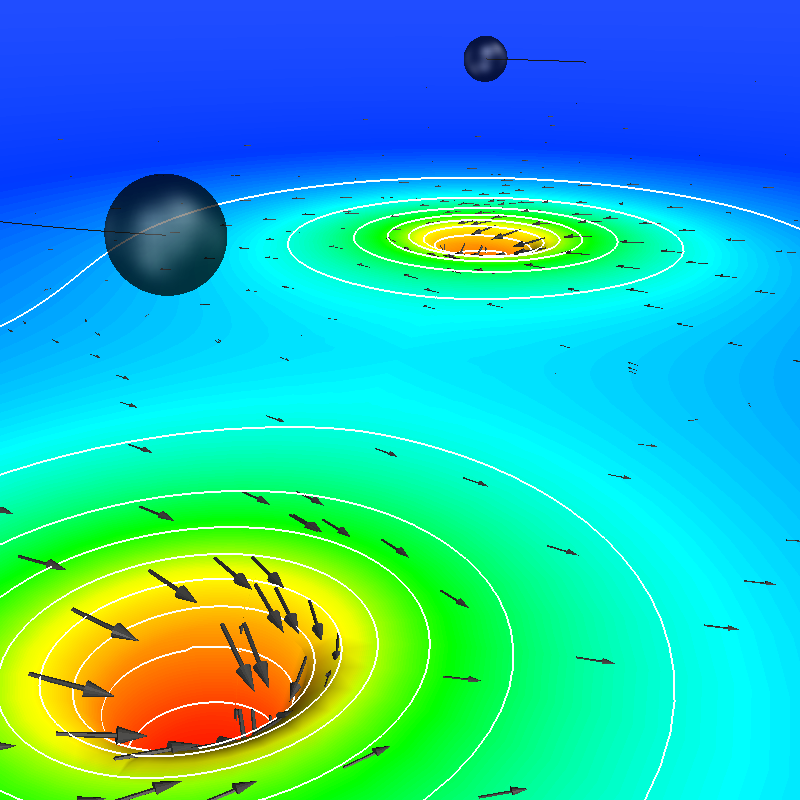
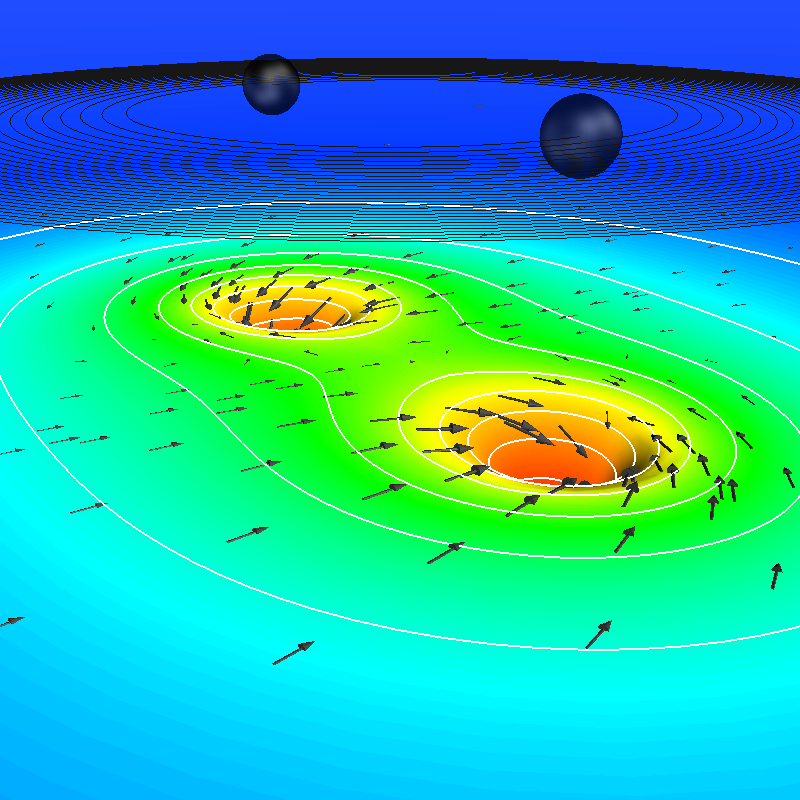
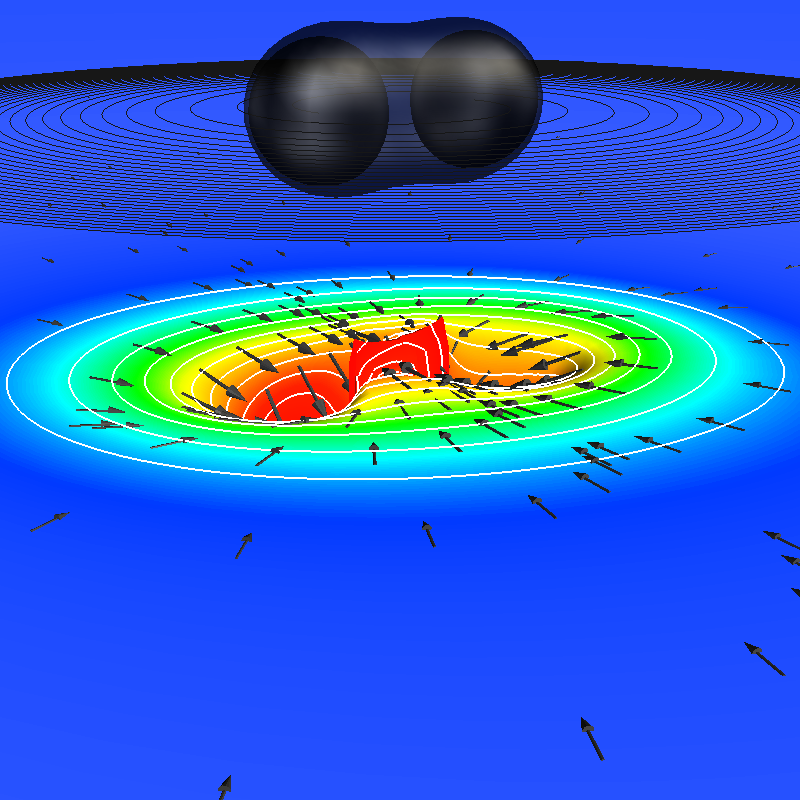

|
|
Simulation of inspiral and merger of two non-spinning black holes (in
collaboration with Numerical Relativity groups at Caltech and Cornell)
|
When black holes collide, they emit a prodigious amount of
gravitational waves, ripples in space-time itself traveling with the
speed of light (gravitational waves are yet another consequence of
Einstein's equations). By observing gravitational waves here
on Earth, we can learn a lot about the objects that made them. Most
importantly (from my view) about black holes, but also about Neutron
stars, supernovae, perhaps even gravitational waves from cosmic
strings or the big bang itself.
| |


|
| |
LIGO gravitational wave observatory (Washington state); illustration of gravitational
waves and the planned LISA spacecraft.
|
Several detectors are already searching for gravitational waves, most
notably the LIGO observatory in the US, but also VIRGO and GEO in
Europe, and TAMA in Japan. Unfortunately, gravitational waves are very
difficult to detect. To make finding the waves easier, it helps to
know the shape of the waves (of, e.g. a binary black hole). To figure
out what one has seen, one must know the shapes of the waves emitted
from different objects (e.g. non-spinning black holes vs. spinning
black holes vs. a Neutron star crashing into a black hole), and
compare to what has been observed. That's where my research
in simulating black holes comes in.

|
|
Domain-decomposition used for the binary black hole evolution.
|
Because of the complexity of Einstein's equations, such computer
simulations require large super-computers to run on, and they require
attention to a lot of details. How does one compute the initial
conditions from which to start? How does one compute how fast the
simulated black holes spin? How does one control the eccentricity of
the orbit of the two black holes ("real" black holes
in the Universe are expected to orbit about each other on almost
perfect circles. So we better simulate such circular binaries, and
not highly eccentric ones). The computer simulations must be highly
accurate, hence a lot of effort goes into making them accurate, and
into ensuring that they are indeed as accurate as we think they are.
Our Spectral Einstein Code (SpEC) is probably currently the fastest
and most accurate code. It is a multi-domain (see picure)
pseudo-spectral method. Nevertheless, I am interested in developing
faster and more accurate computational methods.
| |

|
| |
Space-time diagramm of a mass-ratio 1:6 BBH simulation. Time flows up
in this diagram.
|
After a numerical simulation is completed, one needs to understand
what it means, and what its implication are for data-analysis of the
gravitational wave detectors. Questions like: How well do analytical
perturbation calculations agree with the numerical simulations? (if
paper-and-pencil gives you the answer, there is no need to burn
computer time). How well does LIGO see the computed waves? How can
we use the computer simulations to make LIGO see farther? (in other
words, how can we find weaker signals?) One additional, particularly
cool aspect of the research is development of visualization to help
understand what is going on in the simulations.
Last modified on $Date:: 2009-06-29 #$











